Kā atrisināt kvadrātvienādojumu
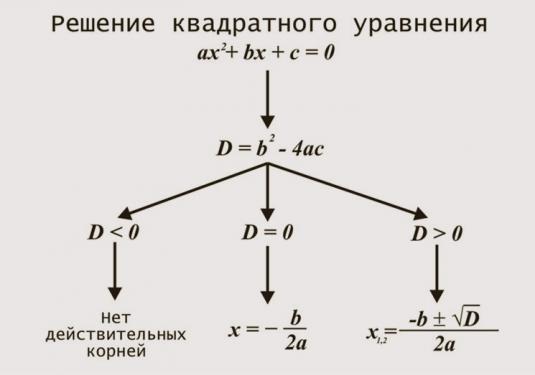
Pilnīgs kvadrātvienādojums tiek atrisināts, atrodot tā diskriminantu.
Atcerieties, ka pilnīgs kvadrātvienādojums ir formas rx vienādojums2+ wx + h = 0, kur r, w, h ir kvadrātvienādojuma koeficienti: daži skaitļi nav vienādi ar nulli, un x ir mainīgais (nezināms).
Kā atrisināt kvadrātvienādojumu caur diskriminantu
Aprēķiniet kvadrātvienādojuma diskriminantu (D). Lai aprēķinātu diskriminantu, no otrā koeficienta w, kas palielināts līdz otrajai jaudai, atņem produkcijas koeficientus r un h ar 4.
D = w2- 4rh
Ja iegūtais kvadrātvienādojuma diskriminētājs ir mazāks par nulli (D <0), tad šim vienādojumam nav sakņu, un tāpēc tam nav risinājuma.
Ja rodas diskriminējošs laukumsvienādojums ir nulle (D = 0), tad vienādojumā ir tikai viena sakne. Lai aprēķinātu šo saknes daļu, ir nepieciešams sadalīt kvadrātvienādojuma w koeficientu ar mīnusa zīmi divreiz par koeficientu r.
Šī ir formula, lai atrastu vienu sakni:
x = -w / 2r
Ja iegūtais kvadrātvienādojuma diskriminētājs ir lielāks par nulli (D> 0), tad vienādojumam ir divas saknes.
Lai atrastu pirmo kvadrātvienādojuma x saknes1, diskriminantora kvadrātsaknei jāpievieno koeficients w ar mīnusu zīmi un rezultāts jāsadala divreiz par koeficientu r.
Lai atrastu x vienādojuma otro sakni2, no diferencienta kvadrātsaknei jāatņem koeficients w ar mīnus zīmi un rezultāts jāsadala divreiz lielāks par koeficientu r.
Ja pilnīga kvadrātvienādojuma forma rx2+ wx + h = 0 ir samazināts, tas ir, koeficients blakus nezināmam otrajā jaudā ir vienāds ar vienību (r = 1), tad to var atrisināt pēc Vī teorēmas formulas.
Kā atrisināt samazināto kvadrātvienādojumu, izmantojot Formulas Vietas teorēmu
Vietas teorēma ir šāda: samazinātās kvadrātvienādojuma sakņu summa ir vienāda ar otro koeficientu, tikai ar pretēju zīmi, un sakņu produkts ir vienāds ar brīvo terminu.
Tas ir, ja vienādojums formas rx2+ wx + h = 0 ir reālas saknes, tad
- x1 + x2 = -w
- x1 * x2 = h
No šīm formulām var mēģināt uzminēt vienādojuma saknes. Lai to panāktu, mums jāpaplašina brīvais termins h divos faktoros, kuru summa būtu vienāda ar koeficientu w ar pretēju zīmi.
Piemēram
Mēs paņemam samazināto x vienādojumu2- 8x + 12 = 0
Mēs to zinām:
- x1 + x2 = 8
- x1 * x2 = 12
Mums ir jāsadala 12 divos šādos faktoros, kas kopā veido 8. Ir skaidrs, ka šādi faktori ir 6 un 2.
Patiešām:
- 6 * 2 = 12
- 6 + 2 = 8
No tā izriet, ka skaitļi 6 un 2 ir patiesisaknes samazinātam kvadrātvienādojumam. Šādi acīmredzami risinājumi ātri nāk prātā, strādājot ar vienkāršiem skaitlisko koeficientu kvadrātvienādojumu. tādēļ vietnes teorēmu bieži izmanto, lai atlasītu kvadrātvienādojumu saknes, kas taupa ievērojamu laiku to risināšanā.