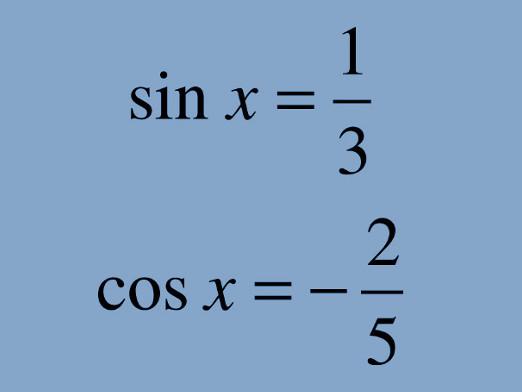Kā atrisināt vienādojumu sistēmas?

Vienādojumu sistēma - no pirmā acu uzmetiena, absolūtibezjēdzīga un nevajadzīga lieta dzīvē. Bet, ja skatāties uz to procesu būtību, kas notiek ap mums, dabā, zinātnes un tehnoloģiju sasniegumos, kļūst skaidrs, ka tas tā nav. Gandrīz jebkura parādība var aprakstīt ar vienādojumu sistēmu, sākot ar lietu pavasarī, beidzot ar asteroīdu lidojumiem kosmosā. Un, kā zināms, var prognozēt fenomenu, kuram ir definēts pietiekami precīzs apraksts.
Kāda ir vienādojumu sistēma
Sistēma ir virkne parastoVienādojumi, kas jāizpilda vienlaicīgi. Uz burtu sistēma tiek apzīmēta ar lencēm kreisajā pusē, apvienojot visus vienādojumus. Un kā atrisināt vienādojumu sistēmu? Sakarā ar to, ka visiem katras norādītās sistēmas vienādojumiem jābūt spēkā kopā, tiek atvērtas vairākas metodes, lai interpretētu, lai pārveidotu sistēmu, nemainot tās saknes. Šādi pārveidojumi tiek uzskatīti par līdzvērtīgiem. Piemēram, ir sistēma "x + y = 2; x - y = 0 ". Acīmredzot tā saknes ir x = 1; y = 1 ". Apskatīsim līdzvērtīgas pārmaiņas.
Papildinājums
Vienādojumu sistēmas atrisināšana ar pievienošanas metodi ir vienkāršākakopā. Mēs pievienojam otro vienādojumu pirmajam vienādojumam un pilnīgi - gan kreiso, gan labo daļu. Mēs iegūstam sistēmu "2 * x + 0 * y = 2 + 0; x - y = 0 ". Pirmajā sistēmas vienādojumā atrodam saknes x = 1. Mēs to aizvietojam ar otro vienādojumu un iegūstam otrā mainīgā lieluma y = 1 vērtību. Sistēma ir atrisināta. Jāatceras, ka pirms pievienošanas vienādojumu var pilnīgi reizināt ar konstantu, kas ir arī līdzvērtīga transformācija. Un šī konstante nav pozitīva.
Aizvietošana
Ja uzdevums izklausās kā "atrisināt sistēmuvienādojumi ar aizstāšanas metodi "- viss ir nedaudz sliktāks. Aizstāšanas metode ir vairāk humomocky nekā pievienošanas metodi, un ne viena lapa var iet uz vienu mazu sistēmu. Lai atrisinātu vienādojumu sistēmu ar aizstāšanas palīdzību, ir nepieciešams veikt vienu no vienādojumu (ērtības labad - pirmais), un izteikt to vienu no mainīgajiem (ērtības labad, pirmais atkal). Vienādojumu no formā "x = 2y + 7z + 9a -2b - 11" Tagad visi citi vienādojumu izvēlēti x to aizvietot ar izteiksme «2Y + 7z + 9a -2b - 11", neaizmirstot vairoties to ar ciparu koeficientu h sākotnējais vienādojums. Mēs iegūstam vienādojumu, kas izteiktu x un vairākus vienādojumus no x nav atkarīgs. Tad mēs veicam līdzīgu darbību visiem mainīgajiem lielumiem. Pēdējā vienādojumā būs skaidri izteikts pēdējais mainīgais, tas ir šīs metodes iezīme. Un tā rezultātā to var atrast. Zinot pēdējo mainīgo, jūs varat aizstāt tā skaitlisko vērtību ar priekšpēdējo vienādojumu un atrast priekšpēdējo mainīgo. Turpinot šādas manipulācijas, jūs varat atrast visus mainīgos lielumus. Lai uzdevumus šādai metodei risināšanā jābūt ļoti uzmanīgiem - tas masa aritmētiskās darbības ir grūti izvairīties no pārpratumiem un novērstu kaitinošas kļūdas. Lai pārbaudītu risinājuma pareizību, varat izmantot pakalpojumu Wolfram Alpha. Tas ir spēcīgs dators centrs, kas var atbildēt uz dažādiem pieprasījumiem, jums tikai nepieciešams, lai aprakstītu problēmu, lai tā saprata datoru. Piemēram, lai sniegtu viņam vienādojumu sistēmu, jums jāievada vienādojumi, atdalot tos ar semikolu.