Kā es varu atrast taisnstūra platumu?

Vienu no problēmām ir atrisināt problēmas ar četrstūriVisizplatītākās ģeometrijas daļas, kas skolēniem rada daudz grūtību. Mēs iesakām risināt tipiskus uzdevumus, kuros vēlaties atrast taisnstūra platumu.

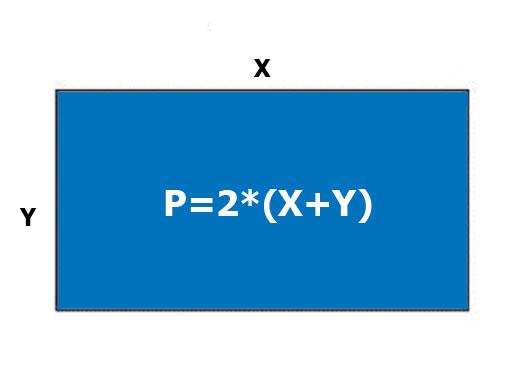
Pirmkārt, ir jāatceras, kāda veidaskaitlis un kādas ir tā galvenās īpašības. Taisnstūris ir četrstūris ar visiem tā leņķiem taisni, un pretējās puses ir vienādas. Horizontālo pusi sauc par taisnstūra platumu, bet vertikālo pusi sauc par garumu.

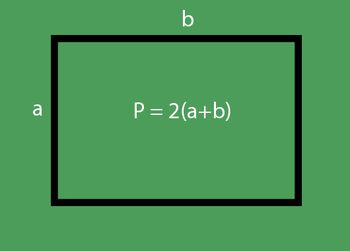
1. problēma. Aprēķiniet platumu, apzinoties perimetru

Ļaujiet mums analizēt šāda veida uzdevumu, izmantojot nākamā uzdevuma piemēru. Taisnstūris, perimetrs

kas ir 36 cm, un garums ir 16 cm. Ir nepieciešams atrast platumu. Perimetrs ir skaitļa sānu summa. Tā kā taisnstūra pretējās malas ir vienādas, tās perimetra formulai ir šāda forma: P = 2 (a + b), kur a un b ir taisnstūra malas.

Mēs iegūstam:

• b = P: 2 - a = 36: 2-16 = 2 (cm)

Atbilde: taisnstūra platums ir 2 cm.

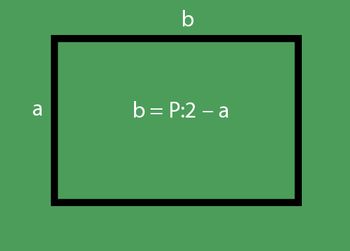
2. problēma. Atrodiet platumu, zinot garumu un perimetru

Let's nedaudz sarežģīt uzdevumu. Tagad mums jāatrod taisnstūra platums, ja ir zināms, ka tas ir 5 reizes mazāks par tā garumu, un trijstūra perimetrs ir 120 cm.

No problēmas stāvokļa:

• a = 5b

Mēs jau zinām, ka b = P: 2 - a. Mēs aizstājam P un a vērtības. Mēs iegūstam:

• b = 120: 2-5b;
• 6b = 60;
• b = 60: 6
• b = 10 (cm).

Atbilde: taisnstūra platums ir 10 cm.

3. problēma. Nosakiet platumu, ja zona ir zināma

Uzdevuma nosacījums: dārzam ir taisnstūrveida forma. Tā platība ir 400 000 m2, un tās garums ir 400 m. Kāds ir dārza platums?

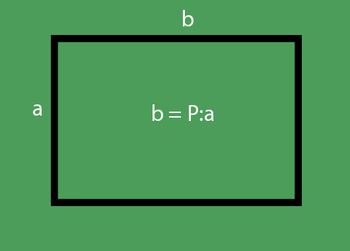
Augu dārzs ir taisnstūris. Taisnstūra laukums ir vienāds ar tā pusēm. Ja mēs zinām garumu un platību, platums būs vienāds ar:

• b = P: a = 400 000: 400 = 1000 (m)

Atbilde: dārza platums ir 1000 m.

4. problēma. Kā atrast platumu, zinot diagonāli

Šis uzdevums jau ir nedaudz sarežģītāks nekā iepriekšējais. Tajā papildus taisnstūra īpašībām būs nepieciešams atsaukt taisnleņķa trīsstūra formulas. Pieņemsim, ka taisnstūra ABCD diagonāli no AC ir 54,6 cm, un garuma un platuma attiecība ir 16: 9. Ir nepieciešams atrast skaitļa platumu.

Trijstūra ABC ir taisnā leņķī, kas nozīmē, ka tas ir taisnstūrveida. Diagonal ir tās hipotenūza, un malas ir kājas.

No nosacījuma:

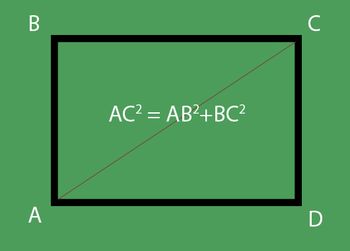
• 16AB = 9BC, tātad AB = 9BC: 16

Ar Pitagoru teorēmu:

• AC² = AB²+ Saule²

Mēs aizstājam skaitļus:

• 54,62 = (9BC: 16)²+ Saule²
• 2981.16 = 81BC²: 256 + Saule²
• 2981.16 = 337BC²: 256
• 337BC² = 763176.96
• Saule² = 2264,62
• VS = 47,59 (cm)

Atbilde: trīsstūra platums ir 47,59 cm.

5. problēma. Diagonāle un leņķis

Parādīts ABCD taisnstūris, kuras diagonāle ir 8 cm, un leņķis ir 30 grādi. Ir nepieciešams atrast taisnstūra platumu.

Risinājums: tā kā ABC leņķis ir taisns, trijstūris ABC ir taisnstūrveida,

hipotenūze, un AB un BC ir kājas. Ir zināms, ka katets, kas atrodas 30 grādu leņķī, ir vienāds ar pusi hipotenūza. Izrādās:

• BC = AC: 2 = 8: 2 = 4 (cm)

Atbilde: taisnstūra platums ir 4 cm.

Kā redzat, tipiskie uzdevumi taisnstūra platuma noteikšanai ir diezgan vienkārši. Galvenais ir zināt taisnstūra un taisnstūra trijstūru formulas un īpašības.

Ja vēlaties atrast taisnstūra garumu, izlasiet rakstu - kāds ir taisnstūra garums.