Kā atrast trapeces pamatu?

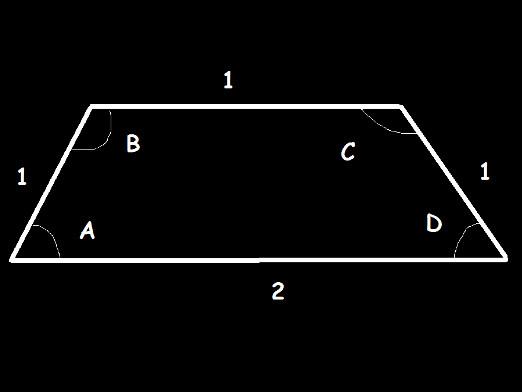
Pirms sākat runāt par to, kā atrastPamatojoties uz trapecveida, ir svarīgi saprast, kas ir trapecveida. Trapecveidā ir ģeometriskā figūra, kas ir četrstūris ar divām paralēlām malām, kas pretojas viena otrai. Šie aspekti matemātikā tiek saukti par trapezes pamatus. Pārējās abas puses sauc par pusēm. Ja savienosim centrālos sānu punktus, mēs iegūstam trapeces viduslīniju. Šīs ģeometriskās figūras īpašības ir visu to raksturlielumu aprēķini.

Lai aprēķinātu trapeces pamatni kā lielu,gan mazie, gan mazie, tiek izmantotas vairākas metodes. Metodes izvēle ir atkarīga no zināšanu apjoma, kas mums ir par objektu. Lielākajā daļā uzdevumu ir nosacījumi, kas satur datus, kas ievērojami vienkāršo problēmas risinājuma meklēšanu. Bieži vien risinājums ir pazemināt augstumu līdz zemei, pielietojot Pitagoras teorēmu, šajā gadījumā problēmu ir viegli atrisināt.

Kā atrast taisnleņķa trapeces pamatni

Tāpat aprēķina bāzivienvirziena trapecveida. Izolēta trapecveida trapecveida ir trapeces forma, kurai ir vienādas sānu malas. Attēlam ir simetrisks skats pret centru, tādēļ tā leņķisko pāri ir vienādi. Tādējādi informācija par vienu stūri vienkāršo uzdevumu aprēķināt visus citus leņķus.

Trapeces sānu daļas ir vienādas ar otru. Piemēram, mums jāatrod zeme, izmantojot šā fonda fragmentu. Otra fragments garumā šajā gadījumā sakrīt ar pirmā fragmenta garumu ar absolūtu precizitāti. Mēs varam arī iegūt nepieciešamo bāzes daļu, izmantojot attēla augstumu, kas veido trīsstūri. Marķējuma parametri un trīsstūra viena puse palīdzēs mums veikt precīzus aprēķinus. Problēmās ir jāatrisina problēma, kā atrast lielāku pamatni vienādainu trapecveida vai mazāku bāzi. Apsveriet piemēru trapezoid mazākās bāzes vērtības aprēķināšanai.

Kā atrast mazāku pamatni ar vienādainu trapecveida

Gadījumā, ja mēs zinām lielākās bāzes lielumu, jautājums par to, kā atrast mazāku bāzes vienādainu trapeciju, vairs nebūs akūts. To var izdarīt šādi:

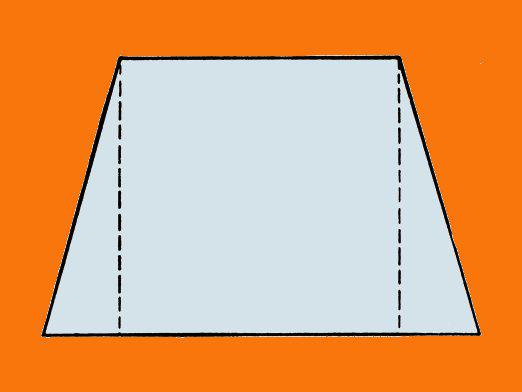
1. Uz lielākas bāzes, augstums ir jāsamazina.
2. Pierakstiet divas Pitagora teorēmas, no kurām vienatiks atspoguļoti trijstūra rādītāji, bet otrs būs vajadzīgs trijstūrim, kas sastāv no hipotenūzes. Pirmajā teorēma gadījumā trijstūrī hipotenūza lomu izpildīs diagonāle, viena kājas loma sasniegs augstumu, bet otrai - lielāka bāze, kam nav segmenta. Segmentu sagriež pēc augstuma. Otro teorēmu izmanto trijstūra, kuras sastāvdaļas ir hipotenūza - puse un katetāte - lielas bāzes iedaļa, kas ir ierobežota ar augstumu.
3. Izstrādā iegūto vienādojumu sistēmu, atrisina tos.
4. Atrodiet segmentu, kas nogriezts no augstuma no lielākā attāluma.
5. Veikt iegūto segmentu divkāršos parametrus no lielākās bāzes parametriem.
6. Iegūstiet rezultātu - mazākās bāzes garums.

Kā atrast taisnstūra trapecveida pamatni

Taisnstūra trapecveida ir sava veida ģeometriskiTrapezium, kura viens leņķis ir vienāds ar deviņdesmit grādiem. Vieglāk aprēķiniet taisnstūra trapeces pamatni. Problēmas stāvoklis, kā parasti, jau ietver datus par otro pamatu. No jums tikai jānosaka bāzes fragments, kas veido cipara leņķi kopā ar malu.

Ar pihagoriešu teorēmu mēs aprēķinām šo daļuIr nepieciešams šo daļu no otrās bāzes pievienot vai atņemt. Aprēķinu rezultātā mēs iegūstam vajadzīgo parametru. Tagad jūs zināt, kā atrast taisnstūra trapecveida pamatni.