Trijstūru līdzības pazīmes

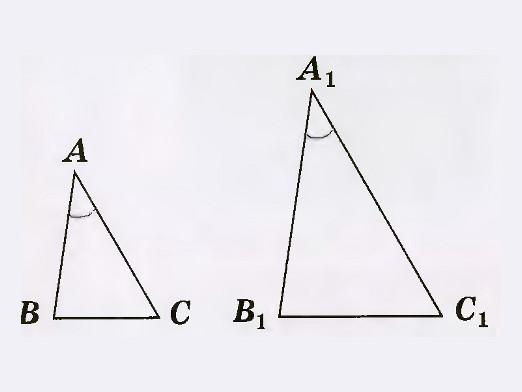
Divu trijstūru līdzības pazīmes ir tādas ģeometriskas iezīmes, kas ļauj konstatēt, ka divi atsevišķi trīsstūri ir līdzīgi viens otram, neņemot vērā visus elementus.

Teorēma 1

Pirmais divu trijstūru līdzības simbols

Trijstūri ir līdzīgi, ja vismaz divi leņķi trīsstūrī ir attiecīgi vienādi ar diviem leņķiem citā trīsstūrī.

Pierādījums.

Ja ir norādīti divi trīsstūra punkti: ABC un A1B1C1, kur ∠A = ∠A1 un ∠B = ∠B1. Tad izrādās, ka ∠C un ∠C1 arī ir vienādas. Ļaujiet mums pierādīt līdzību △ ABC un △ A1B1C1.

Ja mēs atliekam VA pusē segmentu BA2, kassegments būs vienāds ar A1B1, un tad izdarīt taisnu līniju caur A2 punktu, kas ir paralēla līnija AC. Tad šī līnija nogrieza segmentu BC vietā, ko mēs saucam par C2. Tātad, trijstūri un A2VS2 A1V1S1 ir: A2B = A1B1 ar būvniecības ∠V1 = ∠V par stāvokli un ∠A2 = ∠A1 kā ∠A = ∠A1 par stāvokli un ∠A2 = ∠A kā attiecīgajiem leņķiem. Saskaņā ar līdzīgu trijstūru Lemma 1 (līnijas, kas ir paralēla uz vienu pusi no trijstūra un šķērso divas pārējās puses tā, kas nošķeļ trīsstūris, kas ir līdzīgs šim), mums ir: △ ABC ~ △ A2BC2, tādējādi, △ A1B1C1 ~ △ ABC. Tādējādi teorēma ir pierādīta. 2. Un 3. Teorēmu pierāda līdzīga shēma.

Teorēma 2

Otrais trijstūru līdzības simbols.

Trijstūri tiek uzskatīti par līdzīgiem, ja divi no tiemviena trijstūra malas būs proporcionālas attiecīgi otrajam trīsstūra abām pusēm. Tāpat ir jāievēro nosacījums par taisnīguma vienādojumu starp šīm pusēm.

Teorēma 3

Trešā kvadrāta līdzības trešā zīme.

Trijstūri tiek uzskatīti par līdzīgiem, ja tiek ievērots nosacījums, ka proporcija ir no trim pusēm no vienas puses uz otru pusi.

1. piezīme 1. teorēma. Ja mēs uzskatām šādus trijstūrus, tad to līdzīgās puses būs proporcionālas augstumiem, kas tiks izlaisti līdzīgās pusēs.

Taisnleņķa trijstūru līdzības pazīmes

1. taisnstūra formas trijstūri tiek uzskatīti par līdzīgiem, ja katetēts un hipotenūza vienā no tiem ir proporcionāli otrā trīsstūra kājām un hipotenūzi;
2. taisnstūra formas trijstūri tiek uzskatīti par līdzīgiem, ja viens no tiem akūtā leņķī ir vienāds ar otrā trīsstūra īsto leņķi.

Trijstūru līdzības pazīmes piemēros

1. piemērs

Ir nepieciešams atrast segmenta garumu KP, ja tas ir zināmska trijstūrī ABC, AC malas garums ir vienāds ar desmit, un uz sāniem AB ir noteikta vieta K, bet AK = 2 un VC = 3. Pa taisnu līniju ievada caur punktu K, kas ir paralēla AC. Punkts P atrodas tā krustojumā ar pusi BC. Šī ir situācija, kad tiek izmantotas trīsstūra līdzības pazīmes. Katrā skolā vienmēr atrodama stunda ar līdzīgu problēmu. Tātad, ja trijstūris ir līnija novilkta paralēli uz vienu pusi no trijstūra veidojas, kas ir līdzīgs šim. Trijstūris CBS ir līdzīgs trijstūra ABC. Pierādot šo, mēs atzīmējam, ka VRS leņķis ir vienāds ar BAC leņķi. Ņemot vērā faktu, ka tie ir atbilstošie leņķi, kas atrodas paralēli RS un AC un secantam AK. Turklāt, leņķis B - kopējais un līdz ar to trešais leņķi ir vienādi, tad leņķis SDU un BCA. Tādējādi, saskaņā ar teorēmu par līdzīgu trijstūru pirmā zīme, ∠ ABC ∠KVR patīk. No tā izriet, ka RC / AC, sānu guļot pret ∠V arī VC / VA pusē, kas atrodas pretī vienlīdzīgu ∠R un ∠S. Tāpēc mēs atrodam segmentu BA, pievienojot BK un AK. Mēs aizstājam datus, iegūstam: KR / 10 = 3/5, tas ir, KP = 6

2. piemērs

Ļaujiet trijstūros ABC un A1B1C1, ∠B = ∠B1. Abas puses AB, BC trijstūris ABC ir 2,5 reizes lielākas nekā pusēs A1B1, B1C1, kas atrodas trijstūrī A1B1C1. Ir nepieciešams atrast AC un A1C1, ja to summa ir 4,2 m. Šķīdums. Nosakot problēmu, mēs rakstām:

1. ∠B = ∠B1;
2. AB / A1B1 = BC / B1C1 = 2.5 Tāpēc, △ ABC ~ △ A1B1C1. Ar otro apzīmējumu par trijstūru līdzību.
3. AC + A1C1 = 4,2 m. No šo trijstūru līdzības mēs iegūstam rezultātu AC / A1C1 = 2.5 vai AC = 2.5xA1C1. Ja AC = 2,5 x A1C1, tad AC + A1C1 = 2,5 x A1C1 + A1C1 = 4.2, tādēļ AC = 3 (m), A1C1 = 1,2 (m).

3. piemērs

Ir nepieciešams noskaidrot, vai trijstūri ir līdzīgiA1B1C1 un ABC, ja cm, BC = 5 cm, AB = 3, AC = 7 cm, B1C1 = 7,5 cm, A1B1 = 4,5 cm, A1C1 = 10,5 cm? Risinājums. BC / B1C1 = 5 / 7.5 = 1 / 1.5 AB / A1B1 = 3 / 4.5 = 1 / 1.5 AC / A1C1 = 7 / 10.5 = 1 / 1.5

Tādējādi ar trešo apzīmējumu trijstūri ir līdzīgi.