Kā atrast akordu?

Akorda atrašana lokā, pēc būtības -šī ir matemātiska problēma, un vēl jo vairāk, problēma ir no ģeometrijas sadaļas. Tieši tāpēc jau vienkārši zināmu un pierādītu formulu izmantošana ir vienkārši nepieciešama. Turklāt jums jāzina zināmie daudzumi, visvairāk dažādo konstrukciju īpašības lokā un tā elementiem, tikai tad tiks noteikts vajadzīgais segments, kas savieno divus punktus vienā un tajā pašā lokā, saukts par akordu.
Divu punktu savienošana uz apli ar taisnu līniju ir horda. Tātad garākais loku garums ir tā diametrs. Šis akords iet cauri noteiktā apļa centram.
Akorda atrašana
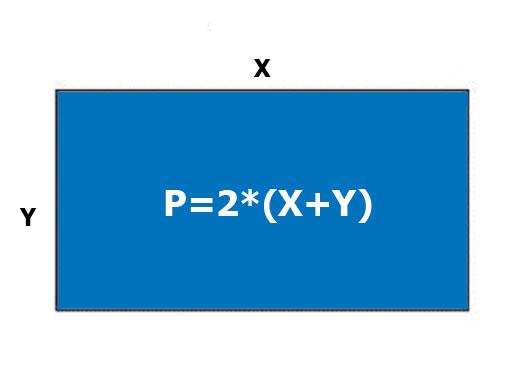
Zināt, kā atrast akordu, tā garums Lir ierasts izmantot formulu L = 2R · sin (x / 2). Ja jūs šo problēmu atrisināt piemērotā veidā, tad jums ir nepieciešams gons, lineāls un transportieris. Ar to palīdzību nosaka stingruma loka garumu, noteiktā apļa rādiusu un leņķi starp rādiusiem, kas novilkti horda galiem.
Lai precīzāk parādītu, kā atrast garumuakordus, jūs varat izmantot piemēru, kurā apļa centrs ir 0, ir horda AB, ir zināms leņķis starp rādiusiem OA un OB-x, apļa R rādiuss un leņķis x. Izveidotais trīsstūris ABO ir vienaldzīgs, jo OA = OB = R. Izmantojot formulu AB = 2 * R * sin (x / 2), tiek iegūts akorda garums AB.
Vēl viens piemērs, ar citu labi pazīstamuparametri, kas palīdzēs saprast, kā atrast horda apļa. Parametri: aplis rādiuss R, DIA garums pie savieno loka, kur C punkts ir uz riņķa vidū A un B. Izmantojot formulu, x ir definēts ar leņķi grādos: x = (ACB * 180) / (pi * R). Tā paliek tikai uz aizvietotāja šajā izpausmes iepriekš, kas iegūts pēc vajadzīgā hordas garums: AB = 2 * R * sin ((ACB * 90) / (pi * R)).
Uz šiem piemēriem var saprast, ka, nosakot divu daudzumu parametrus, kas vajadzīgi horda garuma aprēķināšanai, tos aizvietojot ar formulu, tiek noteikts arī trešais, nezināms daudzums.
Trešais piemērs ir tad, kad ir zināms arī leņķisloka garums R rādiuss nav zināms. Tas būs vienāds ar (ACB * 180) / (pi * x). Tagad iegūtā izteiksme jāaizstāj ar formulu horda garuma noteikšanai: AB = ((ACB * 360) / (pi * x)) * sin (x / 2). Tagad jūs zināt, kas ir akords un kā to atrast. Tas jums palīdzēs atrisināt jebkuru matemātisko un ģeometrisko problēmu.